机器学习算法实践-k近邻算法

K近邻法（KNN）是一种基本的分类方法，它的输入为实例的特征向量，对应于特征空间中的点，输出为实例的类别，可以取多类。实际上是利用训练数据集对特征向量空间进行划分，并作为其分类的模型。

0 k近邻算法的主要学习内容

1）k近邻算法

2）k值的选择

3）距离度量

4）分类决策规则

1 k近邻算法

k=1时,这个算法称为最近邻算法，对于输入的实例点（特征向量）x，最近邻法将训练数据集中与x最近邻点的类作为x的类。k近邻法没有显式的学习过程。

2 k近邻模型

2.1 距离度量[1]

特征空间中两个实例点的距离是两个实例点相似程度的反映，k近邻模型的特征空间一般是n维实数向量空间Rn，使用的距离是欧式距离，但也可以是其他距离。如更一般的Lp距离

例[1]:

2.2 k值的选择

k值的选择会对k近邻法的结果产生重大影响。

如果选择较小的k值，就相当于用较少的实例在进行预测，“学习”的近似误差会减小，因为只有与输入实例距离较近的训练实例才会对预测结果起作用，不足在于“学习”的估计误差会增大，会对近邻的实例点非常敏感，如果近邻的实例点恰巧是噪声，分类预测就会出错，而且k值较小就意味着整体模型会比较复杂，容易发生过拟合。

如果选择较大的k值，就相当于用较多的训练实例来进行预测，虽减少了学习的估计误差，但学习的近似误差会增大，与输入实例较远的不相似的实例也会对预测起作用，使预测发生错误，这时的整体模型变得简单。

如果k=N，那么无论输入实例是什么，都将简单地预测它属于在训练实例中最多的类，这时，模型过于简单，完全忽略训练实例中的大量有用信息，是不可取的。

在应用中，k值一般取一个比较小的数值，通常采用交叉验证法来选取最优的k值。经验规则：k一般低于训练样本数的平方根[2]。

2.3 分类决策规则[1]

k近邻算法的分类决策规则往往是多数表决（少数服从多数），即由输入实例的k个近邻的训练实例中多数类决定输入实例的类。

表示方法：

3 k近邻法的实现

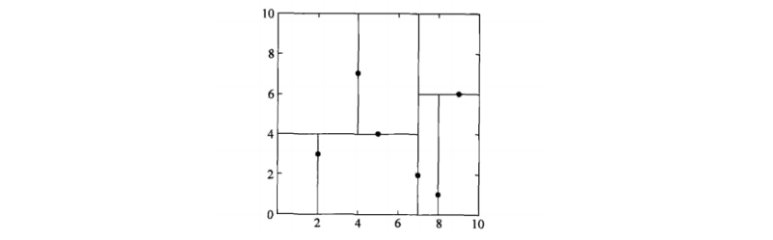
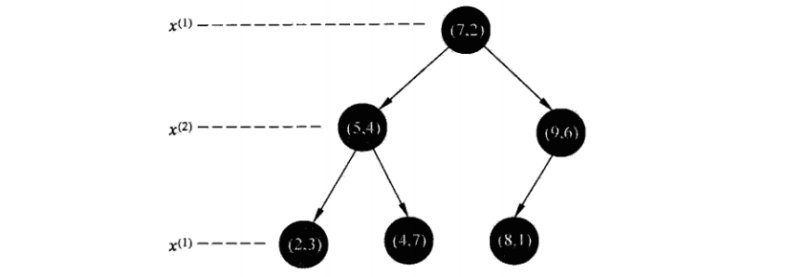
3.1 kd树

实现k近邻算法时，我们主要考虑的问题是如何对训练集进行k近邻搜索，这点在特征空间的维数高，训练数据容量大时尤其必要。为提高k近邻搜索的效率，可以考虑使用特殊的结构存储训练数据，以减少计算距离次数。kd树就有这一作用，kd树是一个二叉树。

例：

3.2 搜索kd树

如图：

kd树适用于训练实例数大于空间维数时的k近邻搜索，当空间维数接近训练实例数时，它的效率会迅速下降，几乎接近线性扫描。

例：

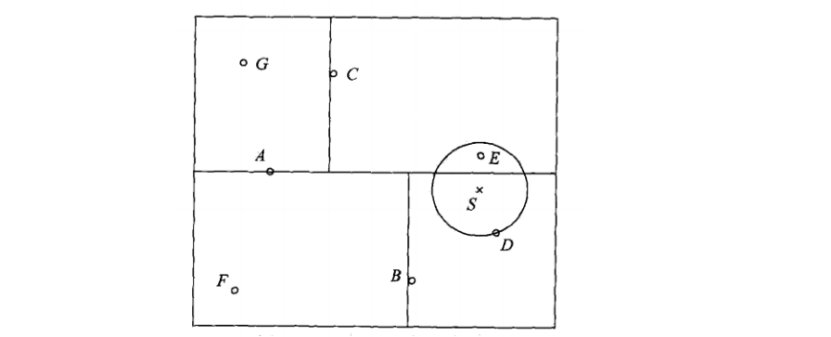
给定一个如图的kd树，根结点为A，其子结点为B，C等，树上共存储7个实例点；另一个输入目标实例点S，求S的最近邻。

解:

首先在kd树中找到包含点S的叶结点D，以点D作为近似最近邻，真正最近邻一定在以点S为中心通过点D的圆的内部，然后返回结点D的父结点B，在结点B的另一个子结点F的区域内搜索最近邻，结果F的区域与圆不相交，不可能有最近邻点，继续返回上一级父结点A，在结点A的另一个结点C的区域内搜索最近邻，结点C的区域与圆相交，该区域在园内的实例点有点E，点E比点D更近，成为新的最近邻近似。最后得到点E是点S的最近邻。

4 k近邻法的总结

4.1 k近邻法的优点

1.简单，易于理解，易于实现，无参数估计，无需训练

2.对异常值不敏感

3.适合对稀有事件进行分类

4.适合样本容量比较大的分类问题

5.适合多分类问题研究，效果有时比支持向量机要好

4.2 k近邻法的缺点

1.懒惰算法，对测试样本分类时的计算量大，内存开销大，评分慢。

2.可解释性不强，无法给出如决策树那样的规则

3.对于小样本的分类问题，会产生误分。

5 k近邻法的应用

1.KNN约会配对

2.K近邻房价评估

3.蛋白质功能检测中的应用

4.网页分类

参考文献

[1] 李航，《统计学习方法》

[2] 常用数据挖掘算法总结及python实现

[3] https://blog.csdn.net/hhy518518/article/details/52840152

[4] https://blog.csdn.net/qq_15258623/article/details/80286230

[5]https://www.docin.com/p-1285931544.html

(部分文字、图片来自网络，如涉及侵权，请及时与我们联系，我们会在第一时间删除或处理侵权内容。电话：4006770986  邮箱：zhangming [at]eefung.com  负责人：张明）